Question

A design engineer wants to construct a sample mean chart for controlling the service life of a halogen headlamp his company produces. He knows from numerous previous samples that this service life is normally distributed with a mean of 500 hours and a standard deviation of 20 hours. On three recent production batches, he tested service life on random samples of four headlamps, with these results: Sample Service Life (hours) 1 495 500 505 500 2 525 515 505 515 3 470 480 460 470 What is the standard deviation of the sampling distribution of sample means for whenever service life is in control? Multiple Choice 5 hours 6.67 hours 10 hours 11.55 hours 20 hours

Answer 1

The standard deviation of the sampling distribution of sample means for whenever service life is in control 10 hours.

Explanation:

The standard error (
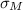`\sigma_(M)`) of the mean is the standard deviation of the sampling distribution of the mean.

The formula to compute the standard error is:

`\sigma_(M)=(\sigma)/(√(n))`

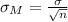
The information provided is:

`\sigma = 20\ \text{hours}\\n=4`

Compute the standard deviation of the sampling distribution of sample means for whenever service life is in control as follows:

`\sigma_(M)=(\sigma)/(√(n))`

`=(20)/(√(4))\\\\=(20)/(2)\\\\=10\ \text{hours}`

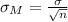
Thus, the standard deviation of the sampling distribution of sample means for whenever service life is in control 10 hours.