Answer:
The value of the appropriate z test statistic to test this claim is 0.48.
Explanation:
We are given that a potential competitor has been conducting blind taste tests on its blend and finds that 48% of consumers strongly prefer its French Roast to yours.
After tweaking its recipe, the competitor conducts a test with 144 tasters, of which 72 prefer its blend.
Let p = proportion of consumers who prefers new blend.
So, Null Hypothesis,
 : p
: p
 48% {means that the new blend is preferred by less than or equal to 48% of consumers}
48% {means that the new blend is preferred by less than or equal to 48% of consumers}
Alternate Hypothesis,
 : p > 48% {means that the new blend is preferred by more than 48% of consumers}
: p > 48% {means that the new blend is preferred by more than 48% of consumers}
The test statistics that would be used here One-sample z proportion statistics;
T.S. =
 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of tasters prefer new blend =
= sample proportion of tasters prefer new blend =
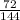 = 0.50
= 0.50
n = sample of tasters = 144
So, test statistics =
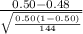
= 0.48
Hence, the value of the appropriate z test statistic to test this claim is 0.48.