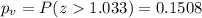Answer:
a) Null hypothesis:
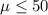
Alternative hypothesis:
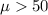
b)
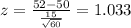
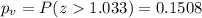
Explanation:
Information suministred
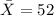 represent the sample mean score for the econd graders
represent the sample mean score for the econd graders
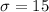 represent the population standard deviation
represent the population standard deviation
 sample size
sample size
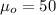 represent the value that we want to test
represent the value that we want to test
z would represent the statistic
 represent the p value for the test (variable of interest)
represent the p value for the test (variable of interest)
Part a: System of hypothesis
We want to check if the second graders in her school district have greater math skills than the nationwide average, the system of hypothesis would be:
Null hypothesis:
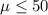
Alternative hypothesis:
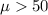
Part b
The statistic is given by:
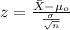 (1)
(1)
Replacing into the formula we got:
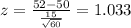
We have a right tailed test then the p value would be: