Question

The local swim team is considering offering a new semi-private class aimed at entry-level swimmers, but needs a minimum number of swimmers to sign up in order to be cost effective. Last year’s data showed that during eight swim sessions the average number of entry-level swimmers attending was 15. Suppose the instructor wants to conduct a hypothesis test and the alternative hypothesis is "the population mean is greater than 15." If the sample size is five, σ is known, and α = .01, the critical value of z is _______.

Answer 1

The significance level is
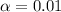`\alpha=0.01` and since we are conducting a right tailed test we need to find a critical value who accumulate 0.01 of the area in the right of the normal standard distribution and we got:

`z_(\alpha/2)= 2.326`

So we reject the null hypothesis is
`z>2.326`

Explanation:

For this case we define the random variable X as the number of entry-level swimmers and we are interested about the true population mean for this variable . On specific we want to test this:

Null hypothesis:
`\mu \leq 15`

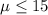
Alternative hypothesis:
`\mu > 15`

And the statistic is given by:

`z =(\bar X -\mu)/((\sigma)/(√(n)))`

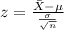
The significance level is
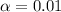`\alpha=0.01` and since we are conducting a right tailed test we need to find a critical value who accumulate 0.01 of the area in the right of the normal standard distribution and we got:

`z_(\alpha/2)= 2.326`

So we reject the null hypothesis is
`z>2.326`