Question

The heat capacity of an object is given by the following equation: C equals 14000 straight J over straight K plus open parentheses 200 straight J over straight K squared close parentheses T plus open parentheses 3 straight J over straight K cubed close parentheses T squared What is the change in the entropy of the object (in J/K) associated with raising its temperature from 290 K to 380 K?

Answer 1

The change in entropy of the object is
`ds = 10.89*10^(4) J/K`

Step-by-step explanation:

From the question we are told that

The equation for the heat capacity is
`C = 14000(J)/(K) + (200 (J)/(K^2) )T + [3 (J)/(K^3) ] T^2`

The first temperature is
`T_1 = 290 K`

The first temperature is
`T_2 = 380 K`

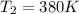
Generally the change in entropy is mathematically represented as

`ds = \int\limits^(T_2)_(T_1) {(dQ)/(T) } \,`

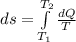
Where dQ is the change in the quantity of heat transferred with time which i mathematically represented as

`Q =C dt`

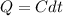
Substituting this above

`ds = \int\limits^(T_2)_(T_1) {(C dt)/(T) } \,`

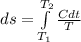
Substituting for C

`ds = \int\limits^(PT_2)_(T_1) {((1400 +200T +3T^2) )/(T) } \, dt`

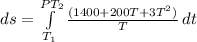
`ds = 1400\ ln [T]+ 200 (T^2)/(T) +3 (T^2)/(2 T) \ \ | \left \ T_2} \atop {T_1}} \right.`

`ds = 1400 ln [(T_2)/(T_1) ] + 200 (T_2 - T_1 ) + (3)/(2) (T_2^2 -T_1^2)`

Substituting values

`ds = 1400 ln [(380)/(290) ] + 200 (380 - 290 ) + (3)/(2) (380^2 -290 ^2)`

`ds = 10.89*10^(4) J/K`