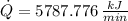Answer:
a)
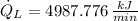 , b)
, b)
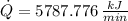
Step-by-step explanation:
a) The efficiency of the Carnot heat engine is:
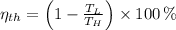
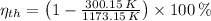
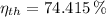
The power output used to drive the refrigerator is:
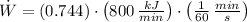
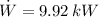
The coefficient of performance of the refrigerator is:
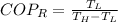
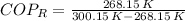
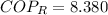
The heat removal from the refrigerated space is:
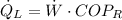

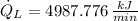
b) The heat rejected from the Carnot heat engine to the ambient air is:
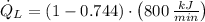
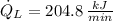
Now, the heat rejected from the refrigerator to the ambient air is:
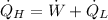
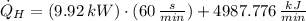

Finally, the total rate of heat rejection to the ambient air is: