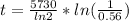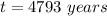Question

The ratio of carbon-14 to carbon-12 in the shaft of a wooden arrow, unearthed when a foundation was being dug for a new house, is 56.0% of the same ratio in a growing tree today. Assuming the ratio of carbon-14 to carbon-12 in the atmosphere has been constant, calculate the age of the arrow. The half-life of carbon-14 is 5730 years. The arrow is _______ years old Numeric Answer:

Answer 1

The wooden arrow is
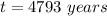`t = 4793 \ years` old

Step-by-step explanation:

From the question we are told that

The ratio of carbon -14 to carbon- 12 is
`n = 56.0`%

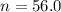The half - life of carbon 14 is
`t_h = 5730 \ years`

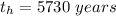
Generally half-life is mathematically evaluated as

`t_h = (ln 2)/(\lambda )`

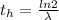
Where
`\lambda` is the decay constant

making
`\lambda` the subject of the formula

`\lambda = (ln2 )/(5730)`

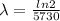
Now the age of the wooden arrow can be mathematically obtained

`t =(1)/(\lambda ) * ln ((Z_o)/(Z) )`

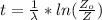
The initial amount of
`Carbon -14` is
`Z_0 = 1`

The amount
`Carbon -14` remaining in the wooden arrow is

`Z = 0.56`%

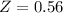substituting values

`t = (5730)/(ln 2) * ln((1)/(0.56) )`

`t = 4793 \ years`