Question

The U.S. Bureau of Labor Statistics released hourly wage figures for various countries for workers in the manufacturing sector. The hourly wage was $30.67 for Switzerland, $20.20 for Japan, and $23.82 for the U.S. Assume that in all three countries, the standard deviation of hourly labor rates is $4.00. Appendix A Statistical Tables a. Suppose 40 manufacturing workers are selected randomly from across Switzerland and asked what their hourly wage is. What is the probability that the sample average will be between $30.00 and $31.00? b. Suppose 32 manufacturing workers are selected randomly from across Japan. What is the probability that the sample average will exceed $21.00? c. Suppose 47 manufacturing workers are selected randomly from across the United States. What is the probability that the sample average will be less than $22.80?

Answer 1

(a) The probability that the sample average will be between $30.00 and $31.00 is 0.5539.

(b) The probability that the sample average will exceed $21.00 is 0.12924.

(c) The probability that the sample average will be less than $22.80 is 0.04006.

Explanation:

We are given that the hourly wage was $30.67 for Switzerland, $20.20 for Japan, and $23.82 for the U.S.

Assume that in all three countries, the standard deviation of hourly labor rates is $4.00.

(a) Suppose 40 manufacturing workers are selected randomly from across Switzerland.

Let
`\bar X` = sample average wage

The z score probability distribution for sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean wage for Switzerland = $30.67

`\sigma` = standard deviation = $4.00

n = sample of workers selected from across Switzerland = 40

Now, the probability that the sample average will be between $30.00 and $31.00 is given by = P($30.00 <
`\bar X` < $31.00)

P($30.00 <
`\bar X` < $31.00) = P(
`\bar X` < $31.00) - P(
`\bar X`
`\leq` $30.00)

P(
`\bar X` < $31) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` <
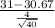`(31-30.67)/((4)/(√(40) ) )` ) = P(Z < 0.52) = 0.69847

P(
`\bar X`
`\leq` $30) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )`
`\leq`
`(30-30.67)/((4)/(√(40) ) )` ) = P(Z
`\leq` -1.06) = 1 - P(Z < 1.06)

= 1 - 0.85543 = 0.14457

The above probability is calculated by looking at the value of x = 0.52 and x = 1.06 in the z table which has an area of 0.69847 and 0.85543 respectively.

Therefore, P($30.00 <
`\bar X` < $31.00) = 0.69847 - 0.14457 = 0.5539

(b) Suppose 32 manufacturing workers are selected randomly from across Japan.

Let
`\bar X` = sample average wage

The z score probability distribution for sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean wage for Japan = $20.20

`\sigma` = standard deviation = $4.00

n = sample of workers selected from across Japan = 32

Now, the probability that the sample average will exceed $21.00 is given by = P(
`\bar X` > $21.00)

P(
`\bar X` > $21) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` >
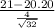`(21-20.20)/((4)/(√(32) ) )` ) = P(Z > 1.13) = 1 - P(Z < 1.13)

= 1 - 0.87076 = 0.12924

The above probability is calculated by looking at the value of x = 1.13 in the z table which has an area of 0.87076.

(c) Suppose 47 manufacturing workers are selected randomly from across United States.

Let
`\bar X` = sample average wage

The z score probability distribution for sample mean is given by;

Z =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\mu` = population mean wage for United States = $23.82

`\sigma` = standard deviation = $4.00

n = sample of workers selected from across United States = 47

Now, the probability that the sample average will be less than $22.80 is given by = P(
`\bar X` < $22.80)

P(
`\bar X` < $22.80) = P(
`(\bar X-\mu)/((\sigma)/(√(n) ) )` <
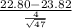`(22.80-23.82)/((4)/(√(47) ) )` ) = P(Z < -1.75) = 1 - P(Z
`\leq` 1.75)

= 1 - 0.95994 = 0.04006

The above probability is calculated by looking at the value of x = 1.75 in the z table which has an area of 0.95994.