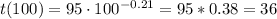Question

An assembled product is built by 10 worker who coordinate their task. A total of 100 units will be made. Time records indicate that the 10 workers took a total of 95 hrs. (unit time) to complete the first unit of the product. Times to complete the second and third units of work are not available; however, the fourth work unit took 71 hr. to complete. Determine (a) the learning rate percentage and (b) the most likely times required to complete the second and third units. (c) If the learning rate continues, how long will it take to complete the 100th unit

Answer 1

a) 86%

b) 2nd unit = 82 hs.

3rd unit = 75 hs

c) 100th unit = 36 hs

Explanation:

We can model the learning curve for manufacturing the units as:

`t=aX^b`

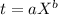
where t is the time for the Xth unit, and a and b are parameters that we will calculate from the data,

We know that t(1)=95. Then, we have:

`t(1)=a\cdot 1^b=95\\\\a=95`

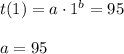
And we know that the fourth unit (X=4) take 71 hours to be completed (t(4)=71). Then, we can calculate the other parameter as:

`t(4)=95\cdot4^b=71\\\\4^b=71/95\approx 0.7473\\\\b\cdot ln(4)=ln(0.7473)\\\\b=ln(0.7473)/ln(4)=-0.291/1.386\\\\b=-0.21`

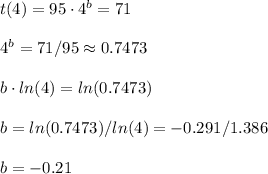
We have the model for the learning curve:

`t=95X^(-0.21)`

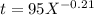
The learning rate percentage is calculated from the b parameter:

`b=(ln(LRP))/(ln(2))=-0.21\\\\\\ln(LRP)=-0.21*ln(2)=-0.21*0.693=-0.1455\\\\LRP=e^(-0.1455)=0.86`

The learning rate percentage is 86%.

b) The most likely times required for the 2nd and 3rd units are calculated with the model:

`t(2)=95\cdot2^(-0.21)=95*0.864=82\\\\t(3)=95\cdot3^(-0.21)=95*0.794=75`

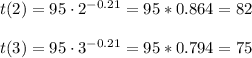
c) If we use the model to calculate the time required for the 100th unit, we have:

`t(100)=95\cdot100^(-0.21)=95*0.38=36`