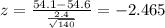Answer:
They want to test if that the claimed MPG is incorrect (different from 54.6 MPG) and this claim needs to be on the alternative hypothesis, so then the system of hypothesis for this case are:
Null hypothesis:
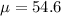
Alternative hypothesis:
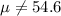
Explanation:
For this case we define the random variable of interest X as the miles per gallon rating. And from a random sample of n = 140 cars we have the following info given:
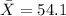
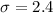
They want to test if that the claimed MPG is incorrect (different from 54.6 MPG) and this claim needs to be on the alternative hypothesis, so then the system of hypothesis for this case are:
Null hypothesis:
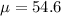
Alternative hypothesis:
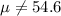
And the statistic to check the hypothesis is given by:
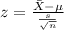
And replacing we got: