Answer:
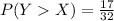
Explanation:
Recall that since X is uniformly distributed over the set [1,4] we have that the pdf of X is given by
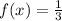 if
if
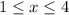 and 0 otherwise. In the same manner, the pdf of Y is given by
and 0 otherwise. In the same manner, the pdf of Y is given by
 if
if
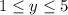 and 0 otherwise.
and 0 otherwise.
Note that if Y is in the interval (4,5] then Y>X by default. So, in this case we have that P(Y>X| y in (4,5]) = 1. We want to calculate the probability of having Y in that interval . That is
 . Thus,
. Thus,
 .
.
We want to proceed as follows. Using the total probability theorem, given two events A, B we have that
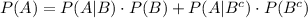 In this case, A is the event that Y>X and B is the event that Y is in the interval (4,5].
In this case, A is the event that Y>X and B is the event that Y is in the interval (4,5].
If we assume that X and Y are independent, then we have that the joint pdf of X,Y is given by
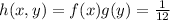 when
when
 . We can draw the region were Y>X and the function h(x,y) is different from 0. (The drawing is attached). This region is described as follows:
. We can draw the region were Y>X and the function h(x,y) is different from 0. (The drawing is attached). This region is described as follows:
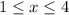 and
and
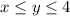 , then (the specifics of the calculations of the integrals are ommitted)
, then (the specifics of the calculations of the integrals are ommitted)
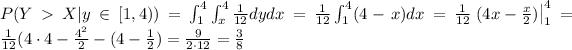
Thus,
