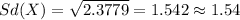Question

A manager at a local company asked his employees how many times they had given blood in the last year. The results of the survey are given below. The random variable x represents the number of times a person gave blood and​ P(x) represents the probability of selecting an employee who had given blood that many times. What is the standard deviation for the number of times a person gave blood based on this​ survey? Round to the nearest hundredth. x 0 1 2 3 4 5 6 ​P(x) 0.30 0.25 0.20 0.12 0.07 0.04 0.02

Answer 1

`Var(X) = E(X^2) -[E(X)]^2 = 4.97 -(1.61)^2 =2.3779`

And the deviation would be:

`Sd(X) =√(2.3779)= 1.542 \approx 1.54`

Explanation:

For this case we have the following distribution given:

X 0 1 2 3 4 5 6

P(X) 0.3 0.25 0.2 0.12 0.07 0.04 0.02

For this case we need to find first the expected value given by:

`E(X) = \sum_(i=1)^n X_i P(X_I)`

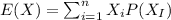
And replacing we got:

`E(X)= 0*0.3 +1*0.25 +2*0.2 +3*0.12 +4*0.07+ 5*0.04 +6*0.02=1.61`

Now we can find the second moment given by:

`E(X^2) =\sum_(i=1)^n X^2_i P(X_i)`

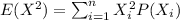
And replacing we got:

`E(X^2)= 0^2*0.3 +1^2*0.25 +2^2*0.2 +3^2*0.12 +4^2*0.07+ 5^2*0.04 +6^2*0.02=4.97`

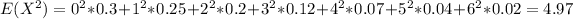
And the variance would be given by:

`Var(X) = E(X^2) -[E(X)]^2 = 4.97 -(1.61)^2 =2.3779`

And the deviation would be:

`Sd(X) =√(2.3779)= 1.542 \approx 1.54`