Question

Extra Credit: Show all your work to obtain credit. A beam of alpha particles ( q = +2e, mass = 6.64 x 10-27 kg) is accelerated from rest through a potential difference of 1.8 kV. The beam is then entered into a region between two parallel metal plates with potential difference 120 V and a separation 8 mm, perpendicular to the direction of the field. What magnitude of magnetic field is needed so that the alpha particles emerge undeflected from between the plates?

Answer 1

B = 0.036 T

Step-by-step explanation:

Given:

`m = 6.64*10^-^2^7`

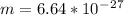
p.d, Va= 1.8 KV = 1800V

Distance btw plates, d= 8mm = 0.008m

`q = 2 * 1.6*10^-^1^9`

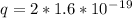
Let's use the equation:

`q*Va = (1)/(2) mv^2`

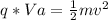
Substitute figures in the equation, we have:

`2*1.6*10^-^1^9 * 1800 = (1)/(2) * 6.64*10^-^2^7 * v'^2`

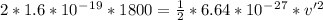
Solving for v' we have:

`v' = 41.65 * 10^4`

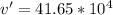
For electric field between plates, we use the formula :

`E = (V)/(d)`

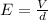
Where V = 120

`E = (120)/(0.008)`

`15*10^3 N/C`

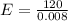
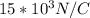
The magnitude of magnetic field, B, needed so that the alpha particles emerge undeflected will be given as:

`B = (E)/(v')`

`B = (15*10^3)/(41.65*10^4)`

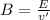
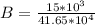
B = 0.036 T