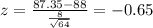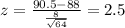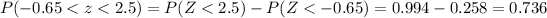Answer:
a)

With:
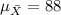
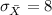
b)
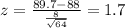
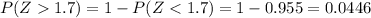
c)
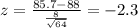
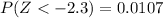
d)
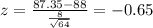
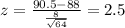
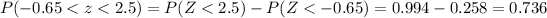
Explanation:
For this case we know the following propoertis for the random variable X
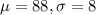
We select a sample size of n = 64
Part a
Since the sample size is large enough we can use the central limit distribution and the distribution for the sample mean on this case would be:

With:
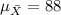
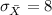
Part b
We want this probability:

We can use the z score formula given by:
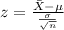
And if we find the z score for 89.7 we got:
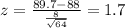
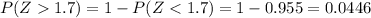
Part c
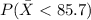
We can use the z score formula given by:
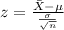
And if we find the z score for 85.7 we got:
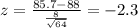
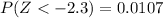
Part d
We want this probability:
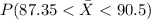
We find the z scores: