Question

Suppose we take a random sample of 41 state college students. Then we measure the length of their right foot in centimeters. We compute a 95% confidence interval for the mean foot length for students at this college. We get (21.71, 25.09). Suppose that we now compute a 90% confidence interval. As confidence level decreases, the interval width ________. Group of answer choices decreases increases stays the same

Answer 1

`ME = (25.09-21.01)/(2)= 1.69`

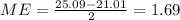
The general formula for the margin of error is given by:

`ME= t_(\alpha/2) (s)/(√(n))`

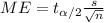
And for this case the width is:

`Width= 2*t_(\alpha/2) (s)/(√(n))`

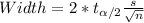
And if we decrease the confidence level from 95% to 90% then the critical value
`t_(\alpha/2)` would decrease and in effect the width for this new confidence interval decreases.

As confidence level decreases, the interval width decreases

Explanation:

For this cae we know that the sample size selected is n =41

And we have a confidence interva for the true mean of foot length for students at a college selected.

The confidence interval is given by this formula:

`\bar X \pm t_(\alpha/2) (s)/(√(n))`

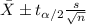
And for this case the 95% confidence interval is given by: (21.71,25.09)

A point of etimate for the true mean is given by:

`\bar X = (21.71+25.09)/(2)= 23.4`

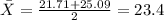
And the margin of error would be:

`ME = (25.09-21.01)/(2)= 1.69`

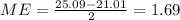
The general formula for the margin of error is given by:

`ME= t_(\alpha/2) (s)/(√(n))`

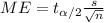
And for this case the width is:

`Width= 2*t_(\alpha/2) (s)/(√(n))`

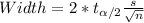
And if we decrease the confidence level from 95% to 90% then the critical value
`t_(\alpha/2)` would decrease and in effect the width for this new confidence interval decreases.

As confidence level decreases, the interval width decreases