Question

In an election to the U.S. Senate, one candidate has popular support of 53% and the other has support of 47%. On election eve, a newspaper will conduct a poll of 750 voters. (a) Compute a normal approximation with continuity correction of the probability that the poll will predict the correct winner. (b) What happens to the probability of correct prediction if they had conducted the poll over only 100 voters?

Answer 1

a) 94.63% probability that the poll will predict the correct winner.

b) 69.15% probability of correct prediction. The lesser sample size leads to more variation, which means that the probability of correct prediction is smaller than in (a).

Explanation:

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

Can be approximated to a normal distribution, using the expected value and the standard deviation.

The expected value of the binomial distribution is:

`E(X) = np`

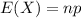
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

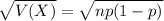
Normal probability distribution

Problems of normally distributed samples can be solved using the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

When we are approximating a binomial distribution to a normal one, we have that
`\mu = E(X)`,
`\sigma = √(V(X))`.

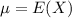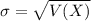(a) Compute a normal approximation with continuity correction of the probability that the poll will predict the correct winner.

The correct winner is the one with 53% of the votes.

We have that
`p = 0.53, n = 750`.

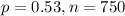So

`E(X) = np = 750*0.53 = 397.5`

`√(V(X)) = √(np(1-p)) = √(750*0.53*0.47) = 13.67`

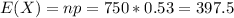
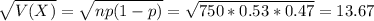
The pool will correctly predict the winner if the candidate that has a support of 53% gets more than half the votes.

So we have to find P(X > 750/2) = P(X > 375)[/tex]

Using continuity correction, this is P(X > 375 + 0.5) = P(X > 375.5), which is 1 subtracted by the pvalue of Z when X = 375.5. So

`Z = (X - \mu)/(\sigma)`

`Z = (375.5 - 397.5)/(13.67)`

`Z = -1.61`

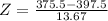
`Z = -1.61` has a pvalue of 0.0537

1 - 0.0537 = 0.9463

94.63% probability that the poll will predict the correct winner.

(b) What happens to the probability of correct prediction if they had conducted the poll over only 100 voters?

Lesser sample size leads to more variation, which means that the probability of correct prediction will be smaller.

Now
`n = 100`

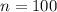
Then

`E(X) = np = 100*0.53 = 53`

`√(V(X)) = √(np(1-p)) = √(100*0.53*0.47) = 4.99`

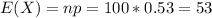
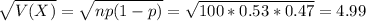
Also P(X > 50), which using continuity correction is P(X > 50.5).

`Z = (X - \mu)/(\sigma)`

`Z = (50.5 - 53)/(4.99)`

`Z = -0.5`

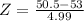
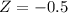
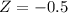`Z = -0.5` has a pvalue of 0.3085

1 - 0.3085 = 0.6915.

69.15% probability of correct prediction. The lesser sample size leads to more variation, which means that the probability of correct prediction is smaller than in (a).