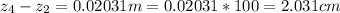Question

A student locates a double-slit assembly 1.40 m from a reflective screen. The slits are separated by 0.0572 mm. (a) Suppose the student aims a beam of yellow light, with a wavelength of 589 nm, toward the slit assembly, and this makes an interference pattern on the screen. What distance (in cm) separates the zeroth-order and first-order bright fringes (a.k.a. maxima)?

Answer 1

Complete Question

A student locates a double-slit assembly 1.40 m from a reflective screen. The slits are separated by 0.0572 mm.

(a) Suppose the student aims a beam of yellow light, with a wavelength of 589 nm, toward the slit assembly, and this makes an interference pattern on the screen. What distance (in cm) separates the zeroth-order and first-order bright fringes (a.k.a. maxima)?

(b)

Now suppose that blue light (with

λ = 415 nm)

is used instead. What distance (in cm) will now separate the second-order and fourth-order bright fringes?

Answer:

a

The distance of separation is
`z_1 - z_o = 1.44cm`

b

The distance of separation is
`z_4 - z_2 = 2.031cm`

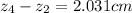
Step-by-step explanation:

From the question we are told that

The distance from the screen is
`D = 1.40m`

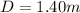
The slit separation is
`d = 0.0572 mm = 0.0572 *10^(-3) m`

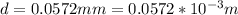
The wavelength of the yellow light is
`\lambda_y = 598nm`

The distance of a fringe from the central maxima is mathematically represented as

`z_n = n (\lambda_y D)/(d)`

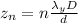
Where n is the order of the fringe so the distance of separation between

The distance that separates first order from zeroth order bright fringe can be evaluated as

`z_1 - z_o = (1 - 0 ) (\lambda_y D)/(d)`

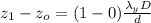
Substituting values

`z_1 - z_o = (1 - 0 ) (590*10^(-9) 1.40)/(0.0572 *10^(-3))`

`z_1 - z_o = 0.0144m`

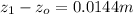
Converting to cm

`z_1 - z_o = 0.0144m = 0.0144*100 = 1.44cm`

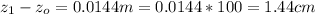
b

The wavelength of blue light is
`\lambda _b`

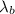
So the distance that separates second order from fourth order bright fringe can be evaluated as

`z_4 - z_2 = (4 - 2 ) (\lambda_y D)/(d)`

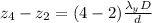
Substituting values

`z_4 - z_2 = (4 - 2 ) (415*10^(-9) 1.40)/(0.0572 *10^(-3))`

`z_4 - z_2 = 0.02031 \ m`

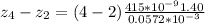
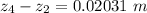
Converting to cm

`z_4 - z_2 = 0.02031m = 0.02031*100 = 2.031cm`