Question

The United States Marine Corps is reviewing its orders for uniforms because it has a surplus of uniforms for tall men recruits and a shortage for shorter men recruits. Its review involves data for 772 men recruits between the ages of 18 to 24. That sample group has a mean height of 69.7 inches with a population standard deviation of 2.8 inches. Construct a 99% confidence interval for the mean height of all men recruits between the ages 18 and 24.

Answer 1

`69.7 -2.58 (2.8)/(√(772))=69.44`

`69.7 +2.58 (2.8)/(√(772))=69.96`

And we can conclude that the true mean for the heights of mens between the ages of 18 to 24 is between 69.44 and 69.7 inches.

Explanation:

For this case we have the following sample size n =772 from men recruits between the ages of 18 to 24

`\bar X= 69.7` represent the sample mean for the heigth

`\sigma=2.8` represent the population standard deviation

We want to construct a confidence interval for the true mean and we can use the following formula:

`\bar X \pm z_(\alpha/2) (\sigma)/(√(n))`

The confidence level is 0.99 or 99%o then the significance level is
`0.01` and
`\alpha/2 =0.005` and if we find for a critical value in the normal tandar ddistirbution who accumulates 0.005 of the area on each tail we got:

`z_(\alpha/2)= 2.58`

And replacing we got:

`69.7 -2.58 (2.8)/(√(772))=69.44`

`69.7 +2.58 (2.8)/(√(772))=69.96`

And we can conclude that the true mean for the heights of mens between the ages of 18 to 24 is between 69.44 and 69.7 inches.

Answer 2

The 99% confidence interval for the mean height of all men recruits between the ages of 18 and 24 goes from 69.44 to 69.96 inches.

Explanation:

The formula for this 99% confidence interval is as follows

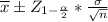`\\ \overline{x} \pm Z_{1 - (\alpha)/(2)}*(\sigma)/(√(n))` [1]

Where

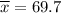`\\ \overline{x} = 69.7` inches, is the mean height of the sample group.

`\\ Z_{1 - (\alpha)/(2)}` is the confidence coefficient.

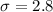`\\ \sigma = 2.8` inches, is the population standard deviation.

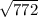`\\ √(772)` is the square root of the sample size, n = 772.

For a 99% confidence interval, the confidence coefficient is about Z = 2.57. That is, for a 99% confidence interval,
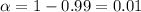`\\ \alpha = 1 - 0.99 = 0.01`. Then

`\\ Z_{1 - (\alpha)/(2)}`

`\\ Z_{1 - (0.01)/(2)}`

`\\ Z_(1 - 0.005)`

`\\ Z_(0.995)`

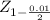
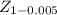
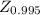
For a probability of 0.995, the corresponding z-score is, approximately, 2.57. So

`\\ Z_(0.995) = 2.57`

Then, having all this information at hand, we can use the formula [1] to "construct a 99% confidence interval for the mean height of all men recruits between the ages 18 and 24".

Thus

Checking again all the values:

• 
  `\\ \overline{x} = 69.7` inches.
• 
  `\\ Z_(0.995) = 2.57`
• 
  `\\ \sigma = 2.8` inches.
• 
  `\\ √(772)`.

`\\ \overline{x} \pm Z_{1 - (\alpha)/(2)}*(\sigma)/(√(n))`

`\\ 69.7 \pm Z_(0.995)*(2.8)/(√(772))`

`\\ 69.7 \pm 2.57*(2.8)/(√(772))`

`\\ 69.7 \pm 2.57*0.10077`

`\\ 69.7 \pm 0.25897`

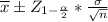
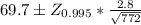
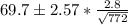
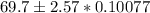
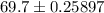
As a result, the upper and lower limits are:

The upper limit is

`\\ 69.7 + 0.25897 = 69.95897 \approx 69.96`

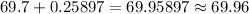
The lower limit is

`\\ 69.7 - 0.25897 = 69.44103 \approx 69.44`

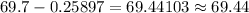
Therefore, the 99% confidence interval for the mean height of all men recruits between the ages of 18 and 24 goes from 69.44 to 69.96 inches.

The result is reasonable since the sample size is large. As the sample is larger, the standard error decreases, so the 99% interval is narrow.