Question

Use the given information to find the ​p-value. ​Also, use a 0.05 significance level and state the conclusion about the null hypothesis​ (reject the null hypothesis or fail to reject the null​ hypothesis). With Upper H 1​: pnot equals​0.377, the test statistic is zequals3.06. A. ​0.0022; reject the null hypothesis B. ​0.0022; fail to reject the null hypothesis C. ​0.0011; reject the null hypothesis D. ​0.0011; fail to reject the null hypothesis

Answer 1

`p_v =2* P(z>3.06)=0.0011`

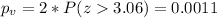
And since the p value is lower than the significance level we have enough evidence to reject the null hypothesia and the best option is:

C. ​0.0011; reject the null hypothesis

Explanation:

For this case we have the following system of hypothesis:

Null hypothesis :
`p=0.377`

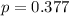
Alternative hypothesis:
`p \\eq 0.377`

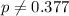
In order to check this hypothesis we can use a z test for a proportion. The statistic is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

And the value for this case is
`z= 3.06`

We are conducting a bilateral test so then the p value can be founded on this way:

`p_v =2* P(z>3.06)=0.0011`

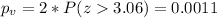
And since the p value is lower than the significance level we have enough evidence to reject the null hypothesia and the best option is:

C. ​0.0011; reject the null hypothesis