Question

In their advertisements, the manufacturers of a diet pill claims that taken daily, their pill will produce an average weight loss of 10 pounds in one month, with standard deviation 3 pounds. In order to determine if this is a valid claim, an independent testing agency selects 36 people to take the pill daily for a month and found the mean weight loss for this group was 9 pounds.

1. Does this indicate at a 5% level that the mean weight loss is less than 10 pounds?

Answer 1

We conclude that the mean weight loss is less than 10 pounds.

Explanation:

We are given that the manufacturers of a diet pill claims that taken daily, their pill will produce an average weight loss of 10 pounds in one month, with standard deviation 3 pounds.

In order to determine if this is a valid claim, an independent testing agency selects 36 people to take the pill daily for a month and found the mean weight loss for this group was 9 pounds.

Let
`\mu` = mean weight loss.

So, Null Hypothesis,
`H_0` :
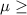`\mu \geq` 10 pounds {means that the mean weight loss is more than or equal to 10 pounds}

Alternate Hypothesis,
`H_A` :
`\mu` < 10 pounds {means that the mean weight loss is less than 10 pounds}

The test statistics that would be used here One-sample z test statistics as we know about the population standard deviation;

T.S. =
`(\bar X-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where,
`\bar X` = sample mean weight loss = 9 pounds

`\sigma` = population standard deviation = 10 pounds

n = sample of people = 36

So, test statistics =
`(9-10)/((3)/(√(36) ) )`

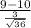
= -2

The value of z test statistics is -2.

Now, at 5% significance level the z table gives critical value of -1.645 for left-tailed test. Since our test statistics is less than the critical value of z as -2 < -1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the mean weight loss is less than 10 pounds.