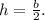Question

The four diagonals of a cube are drawn to create 6 square pyramids with the same base and height. The volume of the cube is (b)(b)(b). The height of each pyramid is h.

Answer 1

It’s 36 i guess:)))))

Answer 2

The volume of the cube is
`\(b^3\)`, and the height of each square pyramid formed by the four diagonals of the cube is
`\(h = (b)/(2)\).`

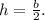
Step-by-step explanation:

The volume of a cube with side length
`\(b\)` is given by
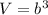`\(V = b^3\)`. In the context of the problem, drawing the four diagonals of the cube creates six square pyramids with the same base as the cube. Each pyramid shares a common vertex with the center of the cube.

The height
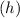`(\(h\))` of these pyramids is equal to half the side length of the cube, i.e.,
`\(h = (b)/(2)\).`

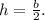
The formula for the volume
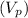`(\(V_p\))` of a square pyramid with base
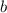`\(b\)` and height
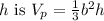`\(h\) is \(V_p = (1)/(3)b^2h\)`. Substituting
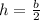`\(h = (b)/(2)\)` into this formula, we get
`\(V_p = (1)/(3)b^2 \cdot (b)/(2) = (1)/(6)b^3\)`.

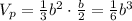Since there are six identical square pyramids formed by the cube's diagonals, the total volume of the six pyramids is
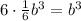`\(6 \cdot (1)/(6)b^3 = b^3\)`. Hence, the final answer is that the volume of the cube is
`\(b^3\)`, and the height of each pyramid is
`\(h = (b)/(2)\).`