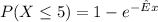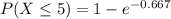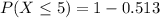Question

The manager of a gas station has observed that the times required by drivers to fill thier car's tank and pay are quite variable. In fact, the times are exponentially distributed with a mean of 7.5 minutes. What is the probability that a car can complete the transaction in less than 5 minutes?

Answer 1

Required probability is 0.487

Step-by-step explanation:

At the gas station the manager perceived that to fill up the tank and payment done by the driver are having variable time. In this circumstance, the intervals are exponentially dispersed with an average of 7.5 minutes.

In this request, the constraint A is the facility time, which is distinct as the average number of facility time per minute.

Let X signify the business interval of a car.

Given the facility intervals are exponentially disseminated with an average of 7.5 minutes.

µ = 1/ʎ= 7.5 min

⇒ ʎ= 1/7.5 min

To compute the probability that car complete transaction less then 5 min

`P(X\leq 5) = 1 - e^(-ʎx)}`

`P(X\leq 5) = 1 - e^(-(1/7.5)5)}`

`P(X\leq 5) = 1 - e^(-0.667)}`

`P(X\leq 5) = 1 - 0.513`

`P(X\leq 5) = 0.487`

Answer 2

48.65%

Step-by-step explanation:

Since the average time it takes car drivers to fill their tanks is exponentially distributed at 7.5 minutes, we can elaborate an exponential formula to calculate the number of times a gas tank can be filled in a certain period of time:

e⁻ˣ/ⁿ

• e = 2.718
• x = 5 minutes
• n = 7.5 minutes

= 2.718⁻⁵/⁷°⁵ = 0.5134

now, the probability that a driver can fill his/her tank in less than 5 minutes = 1 - 0.5134 = 0.4865 or 48.65%