Answer:
a) 177.9 cubits
b) 466137 squared cubits
Explanation:
Given that:
The length of the base (b) = 453 cubits, lateral surface area (a) = 260928, the height of the pyramid (h)
a)
The formula of the lateral surface area is given as:
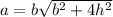
Therefore:
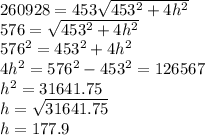
h = 177.9 cubits
b) total surface area = area of base + lateral surface area = b² + lateral surface area
total surface area = 453² + 260928 = 466137 squared cubits