Question

Suppose 240 randomly selected people are surveyed to determine whether or not they play a musical instrument. Of the 240 surveyed, 60 reported playing a musical instrument.

Answer 1

[ 0.19522 < p^ < 0.30478 ]

Explanation:

Solution:-

- A randomly selected sample of n = 240 people are surveyed to determine whether they play any instrument or not.

- The results for the survey showed that that 60 out of 240 people played a musical instrument.

- The proportion of people who played a musical instrument from the surveyed sample is:

p = 60 / 240 = 1/4

p = 0.25

- Where ( p ) is the sample proportion of the number of people who played any musical instrument.

- We are to construct a 95% confidence interval for the population proportion for which we are to determine the Margin of Error ( ME ).

- The general form is given for a confidence interval is:

[ p - ME < p^ < p + ME ]

Where,

p^ : The population proportion

- The margin of error for a confidence interval is given as:

`ME = Z-critical* \sqrt{(p*(1-p) )/(n) }`

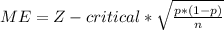
- The Z-critical value is defined by the Confidence level. So for Confidence level of 95% the Z-critical is determined by:

Confidence Level = 95%

Significance Level ( α ) = 1 - CI/100 = 1 - 95/100 = 0.05

Z-critical = Z_α/2 = Z_0.025

Z-critical = Z_0.025 = 1.96

- Therefore the margin of error would be:

`ME = 1.96* \sqrt{(0.25*(1-0.25) )/(240) }\\\\ME = 1.96* \sqrt{(0.25*(0.75) )/(240) }\\\\ME = 1.96* 0.02795\\\\ME =0.05478`

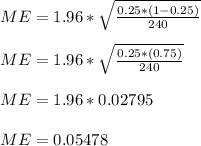
- The confidence can then be written as:

[ p - ME < p^ < p + ME ]

[ 0.25 - 0.05478 < p^ < 0.25 + 0.05478 ]

[ 0.19522 < p^ < 0.30478 ]