Answer:
The perimeter of the figure is 46.3 units, approximately.
Explanation:
To find the perimeter of this figure, we need to use the formula
 , which gives the distance between two points.
, which gives the distance between two points.
Distance of PO.
 and
and
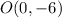 .
.
Using the formula, we have
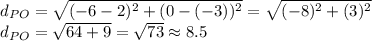
The distance from P to O is around 8.5 units.
Distance of PY.
 and
and
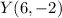 .
.
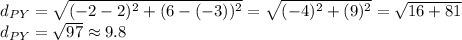
The distance from P to Y is around 9.8 units.
Distance of YR.
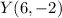 and
and
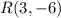
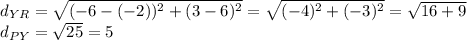
The distance from Y to R is 25 units.
Distance of OR.
This is an horizontal side, we don't need to use the formula. The distance from O to R is 3 units.
Now, the perimeter is the sum of all sides.

Therefore, the perimeter of the figure is 46.3 units, approximately.