Question

Find the limit as xxx approaches positive infinity.
PLEASE HELP

Answer 1

`\displaystyle \lim_(x \to \infty) (3x - 1)/(√(x^2 - 6)) = 3`

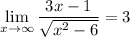
General Formulas and Concepts:

Calculus

Limits

Special Limit Rule [Coefficient Power Method]:
`\displaystyle \lim_(x \to \pm \infty) (ax^n)/(bx^n) = (a)/(b)`

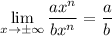
Explanation:

We are given the limit:

`\displaystyle \lim_(x \to \infty) (3x - 1)/(√(x^2 - 6))`

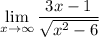
We can see that if we "simplify" the radical, resulting in a degree of 1. Let's use Coefficient Power Method to evaluate the limit:

`\displaystyle \lim_(x \to \infty) (3x - 1)/(√(x^2 - 6)) = (3)/(1)`

Simplifying it, we have:

`\displaystyle \lim_(x \to \infty) (3x - 1)/(√(x^2 - 6)) = 3`

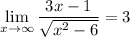
And we have our answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits