Question

Find the limit as xxx approaches negative infinity.

Answer 1

`\displaystyle \lim_(x \to -\infty) (5x^2 + 6x)/(√(16x^4 - 5x^2)) = (5)/(16)`

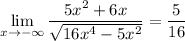
General Formulas and Concepts:

Calculus

Limits

Coefficient Power Method:
`\displaystyle \lim_(x \to \pm \infty) (ax^n)/(bx^n) = (a)/(b)`

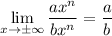
Explanation:

We are given the limit:

`\displaystyle \lim_(x \to -\infty) (5x^2 + 6x)/(√(16x^4 - 5x^2))`

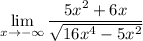
We can see that if we "simplify" the radical, resulting in a degree of 2. Let's use Coefficient Power Method to evaluate the limit:

`\displaystyle \lim_(x \to -\infty) (5x^2 + 6x)/(√(16x^4 - 5x^2)) = (5)/(16)`

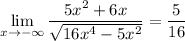
And we have our answer.

Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Limits