Question

Pues, quiero saber cómo simplify ese número.

Answer 1

1.
`2i\sqrt[]{12}`

2.
`3i\sqrt[]{10}`

Explanation:

Lo primero que tienes que saber es que las raíces cuadradas negativas son imaginarias. Luego, resuelve la raíz normalmente pero siempre dejando el signo negativo.

`\sqrt[]{-48}`

Primero pensemos cuáles números multiplican para dar 48.

6 y 8, ahora, como queremos poder eliminar números de la raíz, veamos si hay algún número más que se pueda reescribir de otra forma; por ejemplo, 8 es lo mismo que
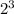`2^3` o
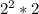`2^2*2`. Como la raíz es cuadrada, siempre buscamos tener números con exponentes cuadrados para poder eliminarlos más fácilmente.

Recordamos también que - es lo mismo que -1

`\sqrt[]{-1} *\sqrt[]{2^2*2*6}` esta es la forma reescrita de la raíz -48.

La raíz cuadrada de -1 es i, porque i significa imaginario. Ahora, Sacamos el 2 que está con exponente cuadrado y dejamos el otro 2 y 6 dentro de la raíz.

`i*2\sqrt[]{2*6}`

Resolviendo y reescribiendo quedaría...

`2i\sqrt[]{12}`

----------------------------------------------------------------------------------------------------------

`\sqrt[]{-90}`

Reescribiendo esto quedaría...

90 es la multiplicación de 30*3 o 15*6 o 10*9

De todos estos, el único que me sirve es 10*9 ¿Por qué? porque 9 se puede reescribir como
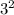`3^2` lo cual eliminaría el 3 de la raíz.

`\sqrt[]{-1}*\sqrt[]{3^2*10}`

Al resolver nos quedaría...

`i*3\sqrt[]{10}`

Ordenándolo...

`3i\sqrt[]{10}`