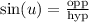Answer:
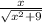
Explanation:
Let
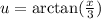 .
.
Then
 .
.
Construct a right triangle.
Make one of the non-right angles
 .
.
Recall
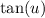 is equal to the ratio of the side that is opposite to
is equal to the ratio of the side that is opposite to
 to the side that is adjacent to
to the side that is adjacent to
 .
.
This means opposite side
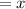 while adjacent side
while adjacent side
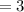 since
since
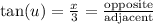 .
.
We can find the hypotenuse by using the Pythagorean Theorem.
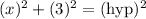
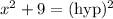
Take the square root of both sides:
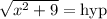 .
.
Recall
 is equal to the ratio of the side that is opposite to
is equal to the ratio of the side that is opposite to
 to the hypotenuse.
to the hypotenuse.
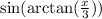
 -->Because we let the inside equal
-->Because we let the inside equal
 .
.
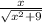 -->Because
-->Because