Answer:
Inverted parabola
Two complex solution
Explanation:
any quadratic equation can be expressed in terms of ax^2 + bx + c = 0
It has two solutions which can be found using formula
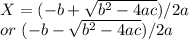
We know that for any value inside the square root function
if it is positive its solution will be real number
for example
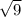 we can have two real solution -3 and 3
we can have two real solution -3 and 3
if it is negative its solution will be complex number
for example
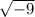 we can have two complex solution
we can have two complex solution
expressed in term of a + ib or a - ib
------------------------------------------------------------------------------------------
Given in the problem
we have ax^2 - bx + c
so its solution will be
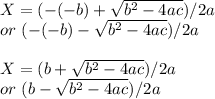
Since in this expression it is given in problem statement that b^2 - 4ac < 0 which will be a negative number and for negative number, its square root is complex number.
also X has two values as given above it will have two solution
hence it will have two complex solution based on above discussion.
Also for any quadratic equation shape of its curve if plotted on coordinate plane is parabolic.
If it has complex solution then curve of such expression will not pass through X axis