We have been given that a ball is thrown into the air. The function
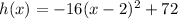 models the height, in feet, of the ball after x seconds.
models the height, in feet, of the ball after x seconds.
We are asked to find the maximum height of the ball.
We can see that our given equation is in vertex form of parabola. We can also see that leading coefficient is negative, so our given quadratic equation represents a downward opening parabola.
Since our parabola is downward opening, so y-coordinate of vertex of parabola will be the maximum height.
Vertex form of parabola:
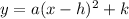 , where point (h,k) represents vertex of parabola.
, where point (h,k) represents vertex of parabola.
Upon comparing our given equation with vertex form, we can see that the y-coordinate of vertex is 72. Therefore, the maximum height would be 72 feet.
Let us write our given equation in standard form
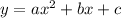 .
.
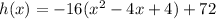
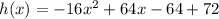
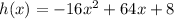
Therefore, standard form of our given equation would be
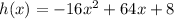 .
.