Answer:
The 95% confidence interval for the standard deviation of the duration times of game play is (279.76, 670.50).
Explanation:
The data for the twelve different video games showing substance use were observed and the duration of times of game play (in seconds) are listed below:
S = {4049, 3884, 3859, 4027, 4318, 4813, 4657, 4033, 5004, 4823, 4334, 4317}
It is assumed that the sample was obtained from a population with a normal distribution.
The confidence interval for population standard deviation is given by,
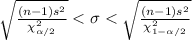
Compute the sample variance s² as follows:
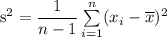
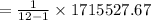
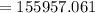
Compute the critical values of Ci-square for 95% confidence level and (n - 1) degrees of freedom as follows:
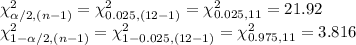
*Use a Chi-square table.
Compute the 95% confidence interval for the standard deviation of the duration times of game play as follows:
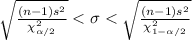
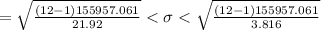
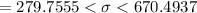
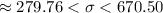
Thus, the 95% confidence interval for the standard deviation of the duration times of game play is (279.76, 670.50).