Question

When people make estimates, they are influenced by anchors to their estimates. A study was conducted in which students were asked to estimate the number of calories in a cheeseburger. One group was asked to do this after thinking about a calorie-laden cheesecake. A second group was asked to do this after thinking about an organic fruit salad. The mean number of calories estimated in a cheeseburger was 780 for the group that thought about the cheesecake and 1,041 for the group that thought about the organic fruit salad.

State the null and alternative hypotheses if you want to determine whether the mean estimated number of calories in the cheeseburger is lower for the people who thought about the cheesecake first than for the people who thought about the organic fruit salad first.

Answer 1

The null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2> 0`

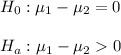
where μ1: mean calorie estimation for the cheesecake group and μ2: mean calorie estimation for the organic salad group.

There is enough evidence to support the claim that the mean estimated number of calories in the cheeseburger is lower for the people who thought about the cheesecake first than for the people who thought about the organic fruit salad first (P-value=0.0000002).

Explanation:

The question is incomplete:

"Suppose that the study was based on a sample of 20 people who thought about the cheesecake first and 20 people who thought about the organic fruit salad first, and the standard deviation of the number of calories in the cheeseburger was 128 for the people who thought about the cheesecake first and 140 for the people who thought about the organic fruit salad first.

At the 0.01 level of significance, is there evidence that the mean estimated number of calories in the cheeseburger is lower for the people who thought about the cheesecake first than for the people who thought about the organic fruit salad first?"

This is a hypothesis test for the difference between populations means.

The claim is that the mean estimated number of calories in the cheeseburger is lower for the people who thought about the cheesecake first than for the people who thought about the organic fruit salad first.

Then, the null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a:\mu_1-\mu_2> 0`

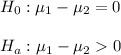
The significance level is 0.01.

The sample 1 (cheese cake), of size n1=20 has a mean of 780 and a standard deviation of 128.

The sample 2 (organic salad), of size n2=20 has a mean of 1041 and a standard deviation of 140.

The difference between sample means is Md=-261.

`M_d=M_1-M_2=780-1041=-261`

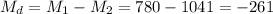
The estimated standard error of the difference between means is computed using the formula:

`s_(M_d)=\sqrt{(\sigma_1^2)/(n_1)+(\sigma_2^2)/(n_2)}=\sqrt{(128^2)/(20)+(140^2)/(20)}\\\\\\s_(M_d)=√(819.2+980)=√(1799.2)=42.417`

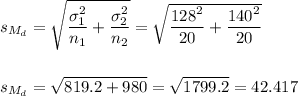
Then, we can calculate the t-statistic as:

`t=(M_d-(\mu_1-\mu_2))/(s_(M_d))=(-261-0)/(42.417)=(-261)/(42.417)=-6.153`

The degrees of freedom for this test are:

`df=n_1+n_2-1=20+20-2=38`

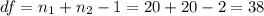
This test is a left-tailed test, with 38 degrees of freedom and t=-6.153, so the P-value for this test is calculated as (using a t-table):

`P-value=P(t<-6.153)=0.0000002`

As the P-value (0.0000002) is smaller than the significance level (0.01), the effect is significant.

The null hypothesis is rejected.

There is enough evidence to support the claim that the mean estimated number of calories in the cheeseburger is lower for the people who thought about the cheesecake first than for the people who thought about the organic fruit salad first.