Answer:
c = 13
Explanation:
Let's first figure out the lengths of RQ and PR. Just count the units.
RQ = 5 units
PR = 12 units
Since we know this is a right triangle, we can use the Pythagorean Theorem. (Or remember that 5, 12, 13 is a Pythagorean triple, so we know PQ = 13!)
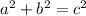
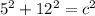

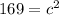
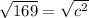
13 = c