Question

A liquid stream containing solute A and carrier liquid C enters a packed column. The solute is to be stripped using pure gas B. The liquid stream enters the column at a rate of 150 kmole/hr and this stream contains 7 mole % A. The stripping gas B enters at a rate of 500 kmole/hr. The design calls for 1 mole % A in the exiting liquid. For the phase equilibrium relationship use yA= 0.4XA. At the conditions of interest we have Kza = 75kmole/(hr *m3)

Determine the height of packing required for this separation if the column cross sectional area is 1m².

Answer 1

the height of packing required for this separation is 15.85 m

Step-by-step explanation:

Given that :

liquid stream (A+C) enters a packed column which the solute is stripped by using a pure gas B

The solute flowrate
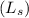`(L_s)` = 150 kmole/hr

Mole fraction of the solute
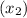`(x_2)` = 7% = 0.07

(A+C)liquid =
`x_1` = 0.01

Pure gas
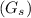`(G_s)` = 500 kmole/hr

`y_1 = 0`

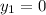
The delivery force in the gas phase & liquid phase is expressed as:

`(K_x)(x_2-x_1) = k_y(y_2-y_1)`

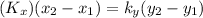
Given that
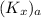`(K_x)_a` = 75 kmole/hr m³ and equilibrium relationship
`y_A = 0.4x_A`

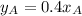
Then :

`K_(xa)(x_2-x_1) = (k_y)_a(y_2-y_1)`

`75(0.07-0.01)=(k_y)_a(y_2-0)`

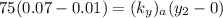
where ;

`y_2 = 0.4x_2`

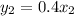
= 0.4(0.07)

= 0.028

`75(0.06)=(k_y)_a(0.028)`

`(k_y)_a = (4.5)/(0.028)`

`(ky)_a = 160.71 \ kmol/hr.m^3`

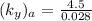
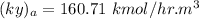
NOW; the overall mass transfer coefficient on the liquid phase is :-

`(1)/((K_(ox))_a) = (1)/((K_x)_a)+ (1)/(m(K_y)_a)`

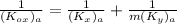
where m= slope = 0.4

`(1)/((K_(ox))_a) = (1)/(75)+ (1)/(0.4(160.71))`

`{(K_(ox))_a} = 34.61 \ kmol/hr.m^3`

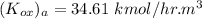
Finally; the height of the tower (z) is =
`(HTU)_(oL)(NTU)_(oL)`

`(HTU)_(oL) = ((L_s)/(s) )/((K_(ox))_a)`

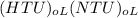
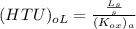
where :

s = 1m²

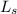`L_s` = 150 kmol/hr

`(HTU)_(oL) = ((150)/(1) )/(34.61)` = 4.33 m

`(NTU)_(oL) = e^x [(((x_2-(y_1)/(m) )/(x_1-(y_1)/(m) ))(1-A)+A )/(1-A) ]`

where A =
`(L_s)/(G_s *m)` =
`(150)/(500(0.4))`

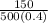
= 0.75

Then:

`(NTU)_(oL) = e^x [(((0.07-0 )/(0.01-0 ))(1-0.75)+0.75 )/(1-0.75) ]`

`(NTU)_(oL) =3.66 \ m`

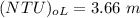
the height of the tower (z) is =
`(HTU)_(oL)(NTU)_(oL)`

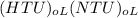
= (4.33)(3.66)

=15.85 m

Thus, the height of packing required for this separation is 15.85 m