Question

In a survey of 1000 randomly selected adults in the United States, participants were asked what their most favorite and what their least favorite subject was when they were in school (Associated Press, August 17, 2005). In what might seem like a contradiction, math was chosen more often than any other subject in both categories! Math was chosen by 230 of the 1000 as the favorite subject, and it was also chosen by 370 of the 1000 as the least favorite subject.

Answer 1

(a) The 95% confidence interval for the population proportion of US adults for whom math was their most favorite subject is (0.204, 0.256).

(b) The 95% confidence interval for the population proportion of US adults for whom math was their least favorite subject is (0.34, 0.40).

Explanation:

The questions are:

(a) Construct and interpret a 95% confidence interval for the proportion of US adults for whom math was their most favorite subject.

(b) Construct and interpret a 95% confidence interval for the proportion of US adults for whom math was their least favorite subject. Solution:

(a)

The 95% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

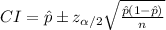
Th information provided is:

n = 1000

Number of US adults for whom math was their most favorite subject

= X

= 230

Compute the sample proportion of US adults for whom math was their most favorite subject as follows:

`\hat p=(230)/(1000)=0.23`

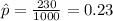
The critical value of z for 95% confidence interval is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

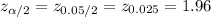
Compute the 95% confidence interval for the population proportion of US adults for whom math was their most favorite subject as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

`=0.23\pm 1.96\sqrt{(0.23(1-0.23))/(1000)}\\=0.23\pm 0.0261\\=(0.2039, 0.2561)\\\approx (0.204, 0.256)`

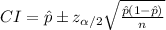
Thus, the 95% confidence interval for the population proportion of US adults for whom math was their most favorite subject is (0.204, 0.256).

(b)

The 95% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

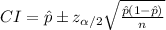
Th information provided is:

n = 1000

Number of US adults for whom math was their least favorite subject

= X

= 370

Compute the sample proportion of US adults for whom math was their least favorite subject as follows:

`\hat p=(370)/(1000)=0.37`

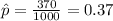
The critical value of z for 95% confidence interval is:

`z_(\alpha/2)=z_(0.05/2)=z_(0.025)=1.96`

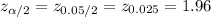
Compute the 95% confidence interval for the population proportion of US adults for whom math was their least favorite subject as follows:

`CI=\hat p\pm z_(\alpha/2)\sqrt{(\hat p(1-\hat p))/(n)}`

`=0.37\pm 1.96\sqrt{(0.37(1-0.37))/(1000)}\\=0.37\pm 0.0299\\=(0.3401, 0.3999)\\\approx (0.34, 0.40)`

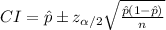
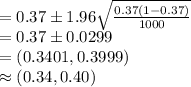
Thus, the 95% confidence interval for the population proportion of US adults for whom math was their least favorite subject is (0.34, 0.40).