Question

100 Points!

Please provide steps.
Solve number 56.

Answer 1

2

Explanation:

∫₀⁴ p / √(9 + p²) dp

If u = 9 + p², then du = 2p dp. So ½ du = p dp.

When p = 0, u = 9. When p = 4, u = 25.

∫₉²⁵ (½ du) / √u

½ ∫₉²⁵ u^-½ du

½ (2u^½) |₉²⁵

√u |₉²⁵

√25 − √9

5 − 3

2

Answer 2

2

Explanation:

`\int\limits^4_0 {p/√(9+p^2) } \, dp`

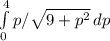
We will use a u substitution

Let u = 9+p^2

du = 2p dp

The lower limit becomes

u = 9+0^2 = 9

The upper limit becomes

u = 9+4^2 = 25

`\int\limits^4_0 {1/2*2p/√(9+p^2) } \, dp`

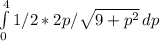
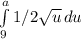`\int\limits^a_9 { 1/2√(u) } \, du` where a is 25

`1/2 \int\limits^a_9 { 1/√(u) } \, du`

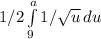
We know the intergral of 1 / sqrt(u) is sqrt(u)/ 1/2

1/2 * sqrt(u)/(1/2) evaluated at 25 and 9

sqrt(u) where u is25 - sqrt(u) where u is 9

sqrt(25) - sqrt(9)

5-3

2