Question

Solve the equation 2x^2 + 16x + 21 = 0 to the nearest tenth.

Answer 1

Rounded to the nearest tenth the solutions to the equation are:

x = -1.7 and x = -6.3

Explanation:

Since this is a quadratic equation of the form:

`ax^2+bx+c=0`

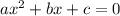
Use the quadratic formula, which tells you that the solutions would be given by:

`x=(-b+-√(b^2-4ac) )/(2a)`

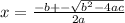
So in our case, the quadratic formula gives:

`x=(-b+-√(b^2-4ac) )/(2a)\\x=(-16+-√(16^2-4(2)(21)) )/(2*2)\\x=(-16+-√(88) )/(4)`

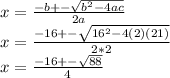
which gives us two real solutions:

x = - 1.654792

x = -6.345207

Which rounded to the nearest tenth give:

x = -1.7 and x = -6.3