Question

1. Undeliverable Mail Pieces. Of the 155 billion mailpieces the U.S. Postal Service (USPS) processed and delivered in 2017, 4.3% were undeliverable as addressed. Suppose that a brief questionnaire about USPS service is attached to each mailpiece in a random sample of 114,250 mailpieces. What is the sampling distribution of the sample proportion of undeliverable mailpieces for this study?

Answer 1

The sampling distribution is, p = center = 0.043

The standard deviation of the sample, s = 6.0015×10⁻⁴

The shape is normal

Explanation:

Here we have the standard deviation of a sample proportion, given by the following relation;

`Standard \ deviation \ of\ \hat p = \sqrt{(p(1-p))/(n) } = \sqrt{(0.043 * (1-0.043))/(114250) } = 6.0015 * 10^(-4)`

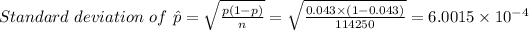
The center = p = 4.3% or 0.043

The shape is found by the value of n×p hence;

114250 × 0.043 = 4912.75 > 10 and

n(1 - p) = 114250 × (1 - 0.043) = 109337.25 also > 10 hence the shape is normal.