Answer:
a1)
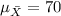
a2)
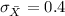
b1)
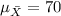
b2)
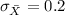
c) X is more likely to be within 1 GPa of 70 GPa in the random sample of part b because of the largeness in sample size and less scattering of data
Explanation:
Mean value,
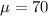
Standard deviation,
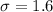
a1) sample size, n = 16
Mean of the sampling distribution of the sample mean = mean value, i.e.
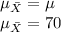
a2) The standard deviation of the sampling distribution of the sample mean

b1) For sample size, n = 64
Mean of the sampling distribution of the sample mean = mean value, i.e.
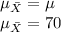
a2) The standard deviation of the sampling distribution of the sample mean
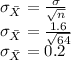
c) X is more likely to be within 1 GPa of 70 GPa in the random sample of part b because it has a larger sample size, hence a decrease in the variability. This makes us easily determine the position of the sample around the population mean