Question

A newspaper article reported that people spend a mean of 6.5 hours per day watching TV, with a standard deviation of 1.7 hours. A psychologist would like to conduct interviews with the 15% of the population who spend the most time watching TV. She assumes that the daily time people spend watching TV is normally distributed. At least how many hours of daily TV watching is necessary for a person to be eligible for the interview?

Answer 1

At least 8.26 hours of daily TV watching is necessary for a person to be eligible for the interview.

Explanation:

We are given that a newspaper article reported that people spend a mean of 6.5 hours per day watching TV, with a standard deviation of 1.7 hours.

A psychologist would like to conduct interviews with the 15% of the population who spend the most time watching TV.

Let X = daily time people spend watching TV

So, X ~ Normal(
`\mu=6.5,\sigma^(2) =1.7^(2)`)

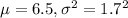The z score probability distribution for normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean time watching TV = 6.5 hours

`\sigma` = standard deviation = 1.7 hours

Now, we have to find that at least how many hours of daily TV watching is necessary for a person to be eligible for the interview, that means;

P(X
`\geq` x) = 0.15 {where x is required number of hours}

P(
`(X-\mu)/(\sigma)`
`\geq`
`(x-6.5)/(1.7)` ) = 0.15

P(Z
`\geq`
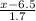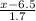`(x-6.5)/(1.7)` ) = 0.15

Since, in the z table the critical value of x which represents the top 15% probability area is given by x = 1.0364, that is;

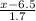`(x-6.5)/(1.7)` = 1.0364

`x - 6.5 = 1.0364 * 1.7`

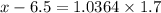
x = 6.5 + 1.762 = 8.26 hours per day

Therefore, at least 8.26 hours of daily TV watching is necessary for a person to be eligible for the interview.