Question

The company has 40 hours of machine time available in the next working week but only 35 hours of craftsman time. Machine time is costed at $100 per hour worked and craftsman time is costed at $20 per hour worked. Both machine and craftsman idle times incur no costs. The revenue received for each item produced (all production is sold) is $200 for X and $300 for Y. The company has a specific contract to produce 10 items of X per week for a particular customer.

Answer 1

$21357

Step-by-step explanation:

The table below gives the number of minutes required for each item

Machine time Craftsman time

Item X 13 20

Item Y 19 29

The company has 40 hours of machine time available in the next working week but only 35 hours of craftsman time. Machine time is costed at $100 per hour worked and craftsman time is costed at $20 per hour worked. Both machine and craftsman idle times incur no costs. The revenue received for each item produced (all production is sold) is $200 for X and $300 for Y. The company has a specific contract to produce 10 items of X per week for a particular customer. Formulate the problem of deciding how much to produce per week as a linear program hence make the decision.

Let be the number of items of and be the number of items of .

We need to maximize:

200 + 300 − 100(ℎ ) − 20( )

subject to:

13 + 19≤ 40(60) ℎ

20 + 29≤ 35(60)

≥ 10

,≥ 0

The object function is now:

`200x + 300y - 100((13x+19y)/(60)) -20((20x+29y)/(60))\\197.1667x+295.8667y\\subject to:\\13x+19y\leq 2400\\20x+29y\leq 2100\\x\geq 10\\x,y\geq 0`

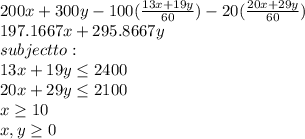
the maximum occurs at the intersection of =10 and 20 + 29≤ 2100.

Solving simultaneously, we have that =10 and =65.52. Substituting in the objective function:

197.1667(10) + 295.8667(65.52)=$21357