Question

Which of the following best describes how the

melted wax will fill the mold? TEKS G11(D)
Adam has a spherical candle with a radius of
2 inches. He melts the candle completely and
pours the soft wax into a mold in the shape of a
rectangular prism. The dimensions of the mold
are shown here.
A
B
2 in
The wax will fill the mold a bit less than
halfway
The wax will fill the mold a bit more than
halfway.
The wax will fill the mold almost perfectly
The wax will fill the mold and there will be a
lot of wax left over
C
D
5 in
5 in.

Answer 1

The wax will fill the mold a bit more than halfway.

Explanation:

The volume of a sphere with radius
`r` is:

`V = \displaystyle (4)/(3)\pi\, r^3`.

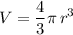The radius of this sphere of wax is
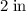`2\;\rm in`; Its volume would be:

`V(\text{sphere}) = \displaystyle (4)/(3)\pi \, r^3 = (4)/(3)\pi* (2\; \rm in)^3 \approx 33.5\; \rm in^3`.

Assume that the wax here does not evaporate, combust, or otherwise disappear.
`V(\text{wax}) = V(\text{sphere}) \approx 33.5\; \rm in^3`.

The volume of a rectangular prism is equal to
`\text{Width} * \text{Depth}* \text{Height}`.

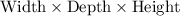For this mold with a rectangular prism shape:

`V(\text{mold}) = (2\; \rm in) * (5\; \rm in) * (5\; \rm in) = 50\; \rm in^3`.

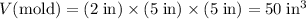Half of that would be:

`\displaystyle (1)/(2)\,V(\text{mold}) = (1)/(2)* 50\; \rm in^3 = 25\; \rm in^3`.

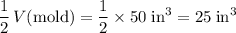Compare these two volumes to the volume of wax available:

`\displaystyle (1)/(2)\, V(\text{mold}) < V(\text{wax}) < V(\text{mold})`.

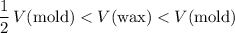In other words, the wax will fill the mold a bit more than halfway, but not completely.