Question

Y = sin(x)
Determine
`y^((123))` (the 123rd derivative of y)

Answer 1

-cos(x)

Explanation:

y¹ = cos(x)

y² = -sin(x)

y³ = -cos(x)

y⁴ = sin(x)

Every 4th derivative is sin(x)

123 = 4(30) + 3

y¹²⁰ = sin(x)

y¹²¹ = cos(x)

y¹²² = -sin(x)

y¹²³ = -cos(x)

Answer 2

Explanation:

Step 1: Find the derivative of the equation four times

`(d)/(dx)(sin(x)) = cos(x)`

`(d)/(dx)(cos(x)) = -sin(x)`

`(d)/(dx)(-sin(x)) = -cos(x)`

`(d)/(dx)(-cos(x)) = sin(x)`

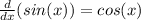
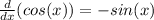
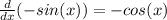
Therefore, every for derivatives that we do, we will get back to sin(x).

Step 2: Find the 123rd derivative of the equation

We are going to have to repeat this cycle for 30 rounds and then, we will have sin(x) as the 120 derivative. Now, we can do it three more times to get the 123rd derivative.

`(d)/(dx)(sin(x)) = cos(x)`

`(d)/(dx)(cos(x)) = -sin(x)`

`(d)/(dx)(-sin(x)) = -cos(x)`

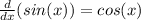
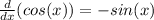
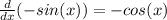
Answer: The 123rd derivative of y is -cos(x)