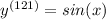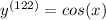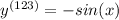Answer:
-sin(x)
Explanation:
We have y = sin(x). The derivative of sin is cos, so:
y' = cos(x)
The derivative of cos is -sin, so:
y" = -sin(x)
Keep doing this, and we'll find a pattern:
y"' = -cos(x)
y"" = sin(x)
Now, we see the pattern; this is a cycle that repeats every 4:
sin(x), cos(x), -sin(x), -cos(x), sin(x), cos(x), -sin(x), -cos(x), ...
That means the derivative of y that is a multiple of 4 will always be equal to -cos(x). 120 is a multiple of 4, which means
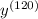 = -cos(x). Then:
= -cos(x). Then: