Question

Dada la ecuacion 25x2 + 4y2 = 100, determina las coordenadas de los vertices, focos, las longitudes de los respectivos ejes mayor y menor, la excentricidad, la longitud de los lados rectos y realiza la representacion grafica

URGENTE

Answer 1

The given equation is

`25x^(2) +4y^(2)=100`

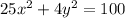
Which represents an elipse.

To find its elements, we need to divide the equation by 100

`(25x^(2) +4y^(2) )/(100) =(100)/(100) \\(x^(2) )/(4) +(y^(2) )/(25) =1`

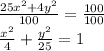
Where
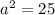`a^(2) =25` and
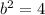`b^(2)=4`. Remember that the greatest denominator is
`a`, and the least is
`b`. So, we extract the square root on each equation.

`a=5` and
`b=2`.

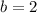In a elipse, we have a major axis and a minor axis. In this case, the major axis is vertical and the minor axis is horizontal, that means this is a vertical elipse.

The length of the major axis is
`2a=2(5)=10`.

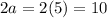The length of the minor axis is
`2b=2(2)=4`.

The vertices are
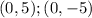`(0,5);(0,-5)` and
`(2,0);(-2,0)`.

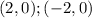Now, the main parameters of an elipse are related by

`a^(2)=b^(2) +c^(2)`, which we are gonna use to find
`c`, the parameter of the focus.

`c=\sqrt{a^(2)-b^(2) }=√(25-4)=√(21)`

So, the coordinates of each focus are
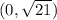`(0,√(21))` and
`(0,-√(21))`

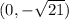
The eccentricity of a elipse is defined

`e=(c)/(a)=(√(21) )/(5) \approx 0.92`

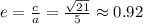
The latus rectum is defined

`L=(2b^(2) )/(a)=(2(4))/(5) =(8)/(5) \approx 1.6`

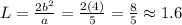
Finally, the graph of the elipse is attached.