Question

If (5x− 4)(3x+ 7) = 15x²-ax-b,then find the value of a and b

Answer 1

`a=-23\\\\b=28`

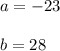
Explanation:

Let's start by using distributive multiplication:

`(a\pm b)(c\pm d)=ac\pm ad \pm bc \pm bd`

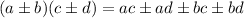
So:

`(5x-4)(3x+7)=15x^2+35x-12x-28\\\\`

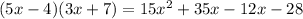
Grouping like terms:

`15x^2 +(35x-12x)-28\\\\15x^2+23x-28`

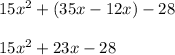
Now,
`15x^2+23x-28` is equal to:

`15x^2-ax-b`

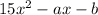
In this sense:

`15x^2+23x-28=15x^2-ax-b`

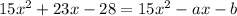
In order to satisfied the equality:

`23x=-ax\hspace{10}(1)\\\\and\\\\-28=-b\hspace{10}(2)`

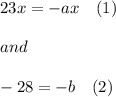
Hence, from (1), let's solve for a:

`23x=-ax\\\\-a=(23x)/(x) \\\\-a=23\\\\a=-23`

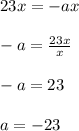
And from (2), let's solve for b:

`-28=-b\\\\b=28`

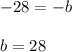
Let's verify the result evaluating the values of a and b into the original equation:

`(5x-4)(3x+7)=15x^2+23x-28=15x^2 -ax -b\\\\(5x-4)(3x+7)=15x^2+23x-28=15x^2 -(-23)x -(28)\\\\(5x-4)(3x+7)=15x^2+23x-28=15x^2 +23x -28`

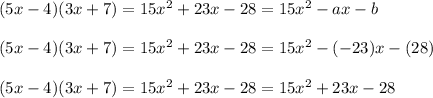
As you can see, the values satisfy the equation, therefore, we can conclude they are correct.