Answer: C. 5,127,079 ft^3
Explanation:
Given : A silo is a composite of a cylindrical tower with a cone for a roof.
Base radius : r = 120 feet
Height of roof ( cone ) h = 25 feet
Total height of silo = 130 feet
Then , height of cylindrical part H= 130 - 25 = 105 feet
Volume of silo = volume of cylinder +volume of cone
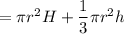
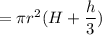
Substitute corresponding values

Hence, the correct answer is C.
 .
.