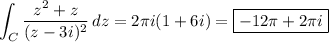First integral:
Parameterize -C (the reverse of C) by
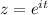 where
where
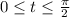 . Then the contour integral is
. Then the contour integral is
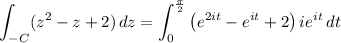
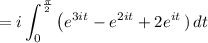
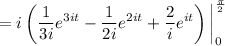
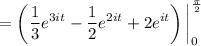
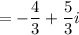
Then
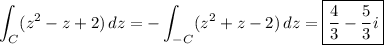
Second integral:
The integrand has a pole of order 2 at z = 3i which is contained in C. By the residue theorem,
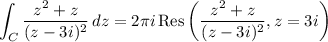
Compute the residue:
![\displaystyle \mathrm{Res}\left((z^2+z)/((z-3i)^2),z=3i\right) = \lim_(z\to3i) (d)/(dz)\left[z^2+z\right] = \lim_(z\to3i) (2z+1) = 1 + 6i](https://img.qammunity.org/2023/formulas/mathematics/college/dw9h3xuyg6vxrvstzlh9nw5v4vu2b100m2.png)
Then the value of the integral is