Answer:
the value of horizontal force P is 170.625 N
the value of horizontal force at P = 227.5 N is that the block moves to right and this motion is due to sliding.
Step-by-step explanation:
The first diagram attached below shows the free body diagram of the tool chest when it is sliding.
Let start out by calculating the friction force
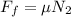
where :
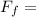 friction force
friction force
 = coefficient of friction
= coefficient of friction
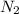 = normal friction
= normal friction
Given that:
 = 0.3
= 0.3
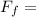 0.3
0.3
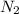
Using the equation of equilibrium along horizontal direction.
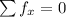
P -
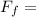 0
0
P = 0.3
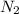 ----- Equation (1)
----- Equation (1)
To determine the moment about point B ; we have the expression
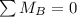
0 =

where;
P = horizontal force
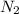 = normal force at support A
= normal force at support A
W = self- weight of tool chest
Replacing W = 650 N
0 =
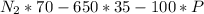

Replacing
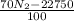 for P in equation (1)
for P in equation (1)
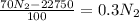
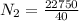
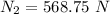
Plugging the value of
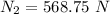 in equation (2)
in equation (2)

P =170.625 N
Thus; the value of horizontal force P is 170.625 N
b) From the second diagram attached the free body diagram; the free body diagram of the tool chest when it is tipping about point A is also shown below:
Taking the moments about point A:
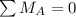
-(P × 100)+ (W×35) = 0
P =
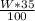
Replacing 650 N for W
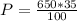
P = 227.5 N
Thus; the value of horizontal force P, when the tool chest tipping about point A is 227.5 N
We conclude that the motion will be impending for the lowest value when P = 170.625 N and when P= 227.5 N
However; the value of horizontal force at P = 227.5 N is that the block moves to right and this motion is due to sliding.